Projections have a wide variety of applications, such as Gram-Schmidt Orthogonalization and dimensionality reduction. In this article, we are going to talk about orthogonal projections. We’ll discuss oblique projections in the future :)
tl:dr
Orthogonal projection πU(x) from vector x∈R² to the 1D subspace spanned by basis vector b is,
Orthogonal projections preserves length.
They have huge applications in various machine learning and scientific applications.
Projection matrices are always symmetric and orthogonal.
Orthogonal Projections
In machine learning, data are represented using matrices. 1D or 2D matrices are easier to imagine and work with. However, as the dimension increases, it becomes increasingly difficult to imagine and compute the data. We can resolve this problem by 'projecting' the higher-dimensional data into a lower-dimensional space where it is easier for us to work without losing any important data. This process is also called dimensionality reduction.
Let's consider projections onto 1D to understand them better.
Projections onto 1D subspace
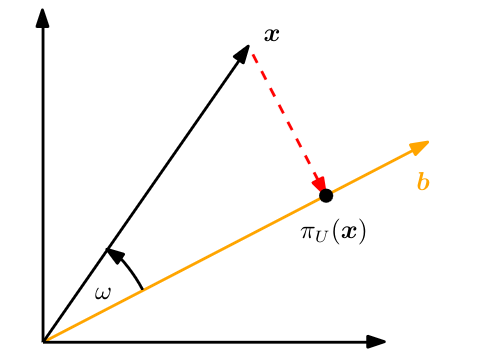
Consider this figure:
As shown in the figure, b is a basis vector that spans a 1D subspace. The vector x belongs to R²(a 2-dimensional space) and we are trying to project x onto b, which is a 1-dimensional subspace. An orthogonal projection is a specific type of linear transformation in which a vector is projected onto a subspace in a way that preserves the orthogonal component of the vector. In other words, an orthogonal projection maps a vector onto a subspace while keeping the part of the vector that is orthogonal (perpendicular) to the subspace.
Since minimum distance is the orthogonal distance from a vector to another , we minimize the distance between the vector x and any vector in the subspace.
Let πU(x) be the projection of shortest distance from x. Then the shortest distance is :
This means the segment is orthogonal to the basis vector b, implying that the inner product (dot product in this case) is 0.
Now lets concentrate on the vector πU(x). This vector can be written as a linear combination of basis vector b. So,
Substituting in eq : 1 , we get ,
Now we can expand this equation using the bilinearity property of the inner product and solve for λ. We will obtain,
Remember that the λ we obtained is a scalar that scales the basis vector b to obtain the vector πU(x). So in order to get the value of πU(x), we have to multiply λ with the basis vector. We can also expand the inner product as dot product.
If we look closely to the equation, we see that why this is a linear transformation of vector x. To understand that, lets rearrange the terms in the above equation :
This is similar to Px, where P is the transformational matrix.
Thus P transforms x onto subspace spanned by b.
We can also infer eq : 2 that P is symmetric because,
Also, P is orthogonal,
Interestingly, the orthogonal projections preservers length because the transformational matrix P is an orthogonal matrix. This means the norm of vector x and the projection of it πU(x) should be same! Lets see,
Since P is an orthogonal and symmetric matrix,
There you go, the norm of projection and the vector is equal!
Next is projections onto General Subspace which I will try to discuss in the next article.
Till then, Bye 👋
Corrections and feedback are appreciated :)